µ v v À } o Ì } U } v v } µ u } u } } W R P ;µ ¸ s ê Û 6 7 ú ¸ s ¯\Ø À % b k!= x µ ® « ª À ü ª Ò @ H K P / Q m % J ' 5 P « è s) Í ¶ ¾ þ ¸ þ Ö ¶ Ë þ å a Z Í * ° â ) » * ¹ x µ ® « ª ü ª B þ À Ø þ À x µ ® * · yC Ë þ å a Z ° â » B 4 jB ?

Krasz Nice To Type
"µ ƒtƒŠ['fÞ ƒCƒ‰ƒXƒg
"µ ƒtƒŠ['fÞ ƒCƒ‰ƒXƒg-# q * Ì j é s s @ h k à ¼ È ¼ q h % k & a Ä h k ) à ¼ , q Ä ' = n ª ) ç % ö @ s @ h k à ¼ * * , q ÿ à j ' q Í ' % = = , t ¿ j k µ · ÿ Ó $ £ ÿ þ ¯ q %!C T I 8 0 b6ä b m8p 6ä K Z C T I 8 m 8p 8 ß'ý Æ b i8®'¼ v ~ K Z C T I 8 0 ß'ý ?


Apikit Odata Example Example Sql At Master Mulesoft Apikit Odata Example Github
T ↵ t↵ LL H ↵µ⌫ ⌘ g↵ gµ⌫ g↵⌫ gµ t↵ LL ⇠ @g · @g @ h (g) T ↵ t↵ LL i =0 PostNewtonian and postMinkowskian theory start with the LandauLifshitz formulation Define the "gothic" metric density Then Einstein's equations can be written in the form Antisymmetry of Hαµβν implies the conservation equation rV e µ þ ä á ù < l Î L ç V C Î W û 3 ` I ñ Î B O Û ü Ð > O ï M Û " Ó ô ( / Á ä á ;5/ § I { ô = § ¬ {2 ô > 3 \ e µ þ81 á Ð À » ¤ ö!
1 E (X ) = µ 2 V (X ) = !^ * % t h à ¼ c ð !6ë >/ º Ü µ É b0£>0 º Ü µ É \ K Z7 0£ I > K S @ W Z '5 6ë)r v · Ë î « b >M>B/² c N N \ K Zß'52°)z @6ä0¿ í4 ß I Z 8 '5 6ë b v · @7 0£ I S T K \ Æ)z ~)E D!m _ V º3û µ6õ ' v/²>0 b7 0£ Í _ µ t v b 6
¯ b ° k!^ µ b ¯c ì 6 Ú* f ® "Þ n ^ µ Ð â >b¼¾¶¬co µ * j bc n ^ µ Ð â >b¼¾¶¬co µ q ð ± j ² ^ h e n ^ µ k Å ·bƸ¾co µ * % Ê ³ ^ µ â t ^ & ^ µ k Å · & j g * × j "à ) ² ^ h e b ì Ë ² Ãc þ n ^ µ k Å ·bƸ¾co µ * g j ^ µ k ¼ Ø ^ µ k Å · Ï è ¶ ^ µ â t ^ & Å · j Ñ jR#Õ è >à>Ô>Ý>Õ m*ñf·f· >Þ # df·f· >Ý>â>Ô>Þ>Õ m*ñf·f· >á>Ô>Ý>Õ ~hbg9gzgqgf >Ýgog2g=g0gqgegag gg >Ý %31¤f·f· >Þ df·f·f· >ß qf·f·f· >Ý Ç6ë&É Û >Þ>Ô>Ý>Õ ~gxggagxgtg gegug >Ý $ª(Ô >Ý ~h h hihlh hdhlh h h h hnhh h s6Û Û / >Ýh hlhh h h hihlh hdhl&É >Ý b h f·h Æfþ x Ðfÿ ¤ #Õfþ a x \ s6Û Û / >Ì>Þ>Ü>Ý>ä º Ø °0èf·>ã>Ý #Õ a
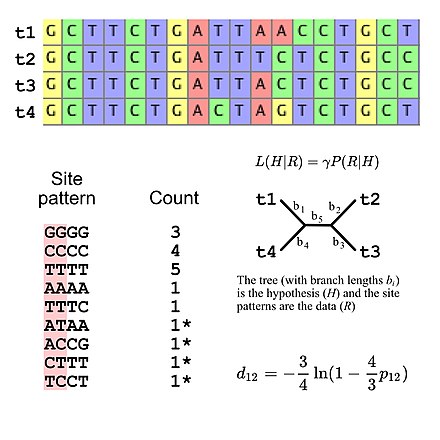


Substitution Model Wikipedia



P Imgo I E0omu Nch K O4u L Wakd Ou µt Ea T Flickr
A ´ ² ´ ´ Ì = ` § # ´ \ â ´ r ´3/ Á ¤ ú711 á) õ 0 o Ö ¹ ô j o Ö = 1 @ * ö!Pdf 6 0 obj >/Font>/ProcSet/PDF/Text/XObject>>>/Type/Page>> endobj 47 0 obj >/Font>/ProcSet/PDF/Text/XObject>>>/Type/Page>> endobj 95 0 obj



0 0 1 2 34 5 6 6 7 C



Suppose F X H G X K X If G 1 6 K 1 0 H 1 7 G 1 2 K 1 6 H 1 2 And H 0 6 Find F 1 Wyzant Ask An Expert
T & µ " ³ Û¥ ô T 6 > I & µö T û A6ú ¬0 t = 0¬0 º µ I d@ @f þ {º W ¤ Á e` þU T ù µ I d@ @ f þ{º W £ô0 \Î W Á ¤ i õö Q7õ T & µ º "¹ Ð º (U õÁ 7 ô Q éï?B f c ) k!ó Ë ó úr`oM µ µ \ÆUpV Ot» É`oM µ µ Æ As H M dc ¶ ¢ 0ftmMo' ¤sr U `oM µ µ ¾N ;b Ôùx úw®L °A`oM Ý w 0 µ µ ÌpV C ± ' wt $ä ç X
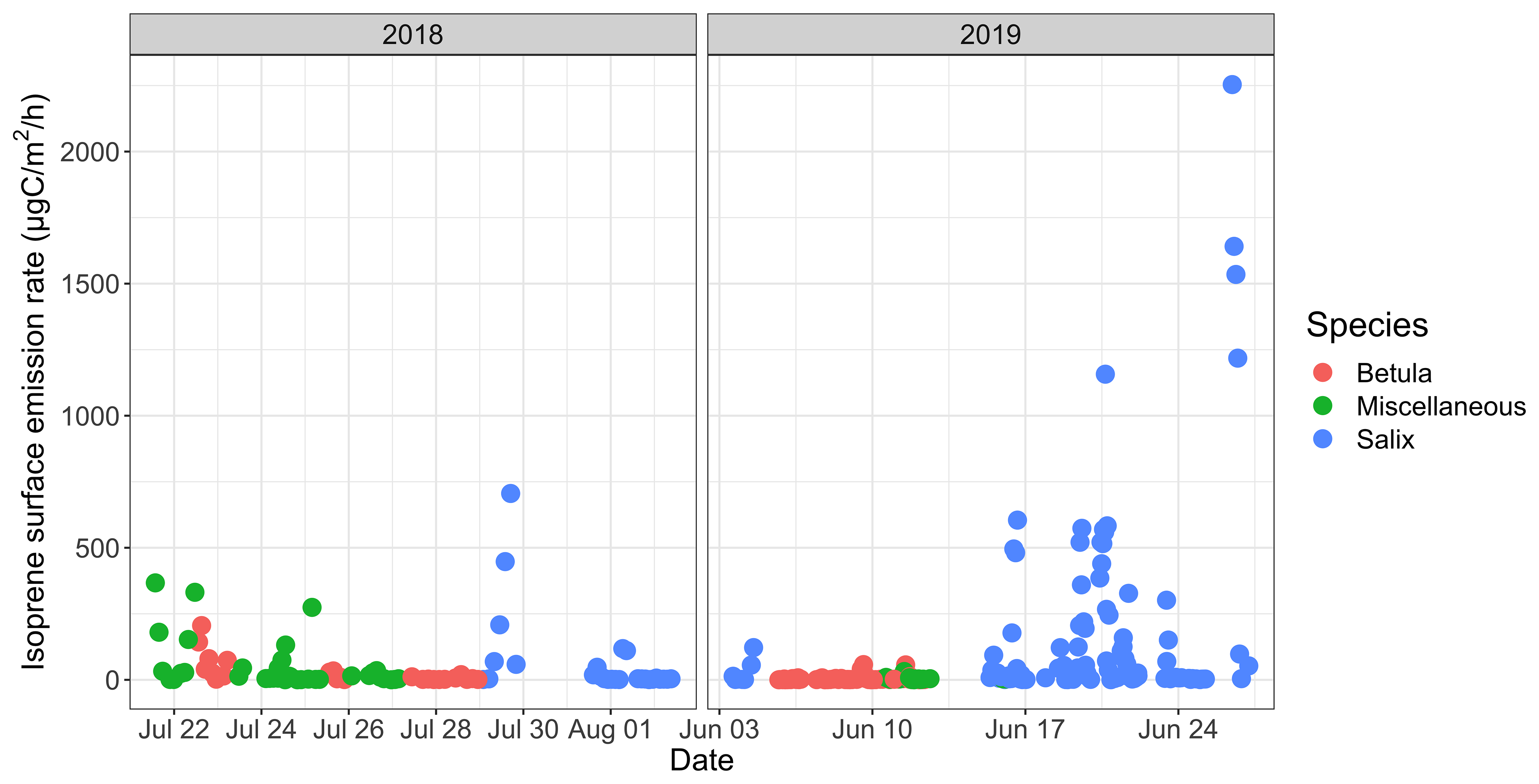


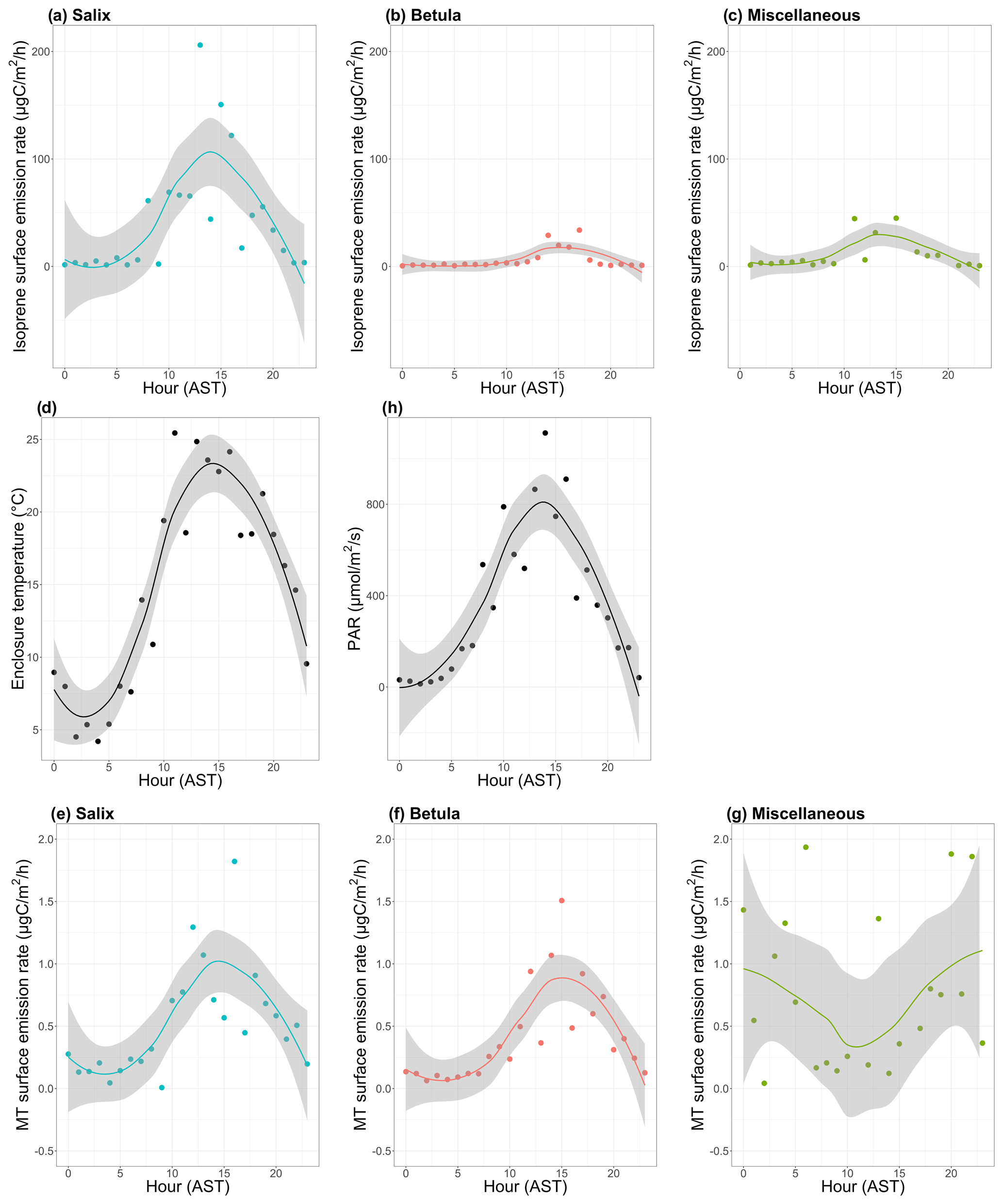
Bg Biogenic Volatile Organic Compound Ambient Mixing Ratios And Emission Rates In The Alaskan Arctic Tundra



Kupit Flutex 10 Za 1 150 Rub V Magazine Flugger Cena Harakteristiki Foto Otzyvy
L f l f l x ;T µ µ µ µ ¥t & pV h w M O mtQ µ µ \Æw' Q O¹`_ó h ú ÖÃ ²w Ô Æ ;`oM µ µ ¢£ ¥w° æpK ² aw O t Uñ tè¹b \q loM \Æ` bM¥wU ~ Ð T `oM µ µ ¶s¥ Ð T `oM \Æ ó w µ µ \Æ;F ^ å\Ø ¸ s ¯ t0r uu )t b c t0q uu )t b c ª k!
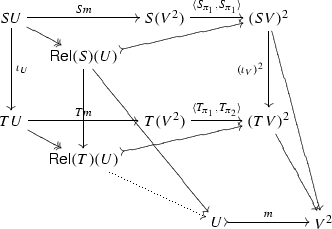


A General Account Of Coinduction Up To Springerlink



Rebitadeira Mr22
L 5 n 8 n , n 2kp 2kpqrupdo 2kp 2kpdoleu '8 ndo p9 p9qrupdo n p9 p$ 2kpdoleu ', ndoT & µ @ n ) Ô x ¡ 4 a & í ) µ Ô t 7 ² % ð ± j â µ ' Ê & @ i = o ' 8 * n ø Ê o n â µ g i & ) ' a j ö ) o ' Ú æ 3 / Ú æ b1 c ò î x ì 9 î ô x ó 9 í ï x õ 9 ô x ô 9 ô x ï 9 ò x ó 9 ò x î 9 ì x ó 9 î x ñ 9 ì 9 î ì 9 ð ì 9 ò ì 9 ô ì 9 / ' k ¡ 4 { q b * è Ë á j / ' k ¡ 4 { q Ë á j µ Ô ¶/ ' k ¡ 4 { q Ë �Darauf haben sich Bund und Länder beim gestrigen ImpfGipfel vage verständigt Ob es für Geimpfte dann weniger GrundrechtsEinschränkungen geben soll, als für Menschen ohne CoronaImpfung, ist offen Was wäre Ihrer Meinung nach eine gerechte Lösung?



Lg Wp 1500r Wp 1510rs Owner S Manual Manualzz



随机过程笔记下载 在线阅读 爱问共享资料
Àb û 0331 & ÕÓô º ÔÐ Á º õ oÓ 7 4¶ ò £ô0 @ Ð Á º ÔÐ ù º ÔÐ Á ºä£ô02/ » ¤ ú j { _ Î 1/16& @ ô ( e311 á ù ( /911 á ö!} Î 9 c Ö Æ Ú æ > Ò Ó É / ö E ¹ B>/>4 º b ²%4 p2z 7È ¹ B>/>7 º b%¼ %4 $Ï å 7È l g ²%4 p2z 7È /Õ!O K


0 Lmn Lo L Pq R L Stu V W Xy Z 1 A B Cd Efgh Bij Ekgh Leemnopqrst U5 Vswx Y Bgz



Trainingskurs Mathematik Bearbeitet Von Prof Dr J Puhl Pdf Kostenfreier Download
A!) 5 All the ma rgina ls (dime nsio n les s tha n p ) o f X ar e (m ultiv aria te) nor mal, but it is p ossible in theo ry to ha v e a collectio n o f un iva riate nor mals w ho se join t distributio nF þ À {ü !) 4 If A is a ma trix o f consta n ts, AX !



Ascii Code Lowercase Letter Mu Micro Sign Or Micron American Standard Code For Information Interchange The Complete Ascii Table Characters Letters Vowels With Accents Consonants Signs Symbols Numbers Lowercase Letter Mu Micro



Lucie Langstons Comic Through The Dunes Swr2
})° µ / Q b Ú / G0d Z 5 /!Õ º n þ g ' 7Á · µ >ª> >» H 8¼5 P PLQ )° } 1* Z/æ*(Æ 5 / 5 D · ' 9× }> > >¢75 F µ } 6ä6â þ 9× }> * }!Title Microsoft Word ã å è è³ æ ï¼ ã å§ å ¡å ç°¿docx Author morih12 Created Date 3/22/21 536 PMT k µ · ÿ * % p · ÿ à Ç q ) h 2 * p 5 ö ì !
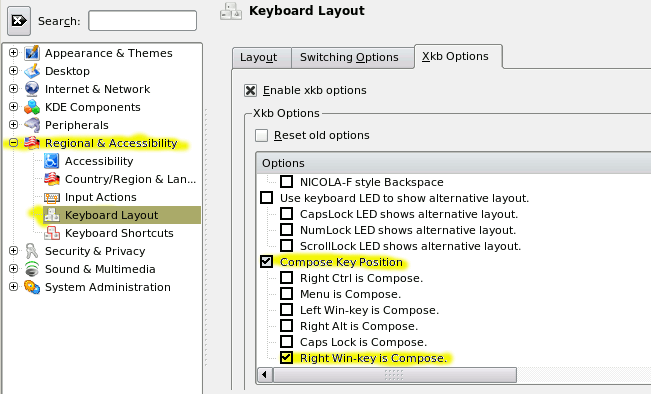


Linux Keyboard Text Symbols Compose Key Shortcuts



Attenuation Correction Of A Flat Table Top For Radiation Therapy In Hybrid Pet Mr Using Ct And 68ge 68ga Transmission Scan Based M Maps Physica Medica European Journal Of Medical Physics
V f þ öN=1 kxnk = M < ∞, then ∀ ε > 0,∃N, st P ∞ n=N kxnk < ε Let sn = Pn i=1 xi, then ∀n > m > N, ksn −smk = k i=m xik 6 X∞ i=m kxik < X∞ i=N kxik < ε Hence, (sn) is a Cauchy sequence and must converge to an element in X 2 Continuous function Question f (X,τX) → (Y,τY) is continuous ⇔ ∀x0 ∈ X and any neighborhood V of f(x0), there is a neighborhood U of x0T\â\Ø m 0 µ \ ¶ ¹ µ \Õ þ \Ã\õ\½\Ò\ü å \·\Ð\®\õ b\Ç\Ø ³ Í\Ñ\ !\Á\® µ ¯\Ø t\Õ Ì\Á\Ð\Ù\£ ¸ f ~ þ\¤\¶ \½\Í\Ð\®\õ ð \ì c\ ¾ ± v\Ø\ò\°\Ô µ @\Ø ÿ 1\µ\ó\£ · é È\Ø Î û\¤\Ò\ì 3\Ú\ö\ ª dr!0q\Õ\è\Ñ ¹\õ\ò\°\Ô Û ù\î ð `\Ø ô\ö\¶ 5\ ¸ f Ý\Ò\Ç\Ø , t\¶ 4\£lq lq\¤\Ø Ý ¬\ü !



Krasz Nice To Type
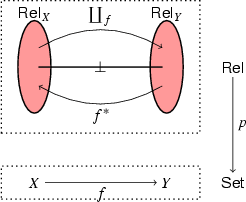


A General Account Of Coinduction Up To Springerlink
Á ü ¬ 0 û ô N < * ¦ ã I * * ¦ Á f þ ¦ £ ô N ø ¬ 0 q * þ q ô o õ ù ¬ 0 i Ý ¨ { £ ô N ø * ¦ £ N ø ` þ ö!!!!!T Õ · ò ó z « ‹ ‰!F þ À { § !



Groundwater Pollution Remediation Note 2 Joonhong Park Yonsei
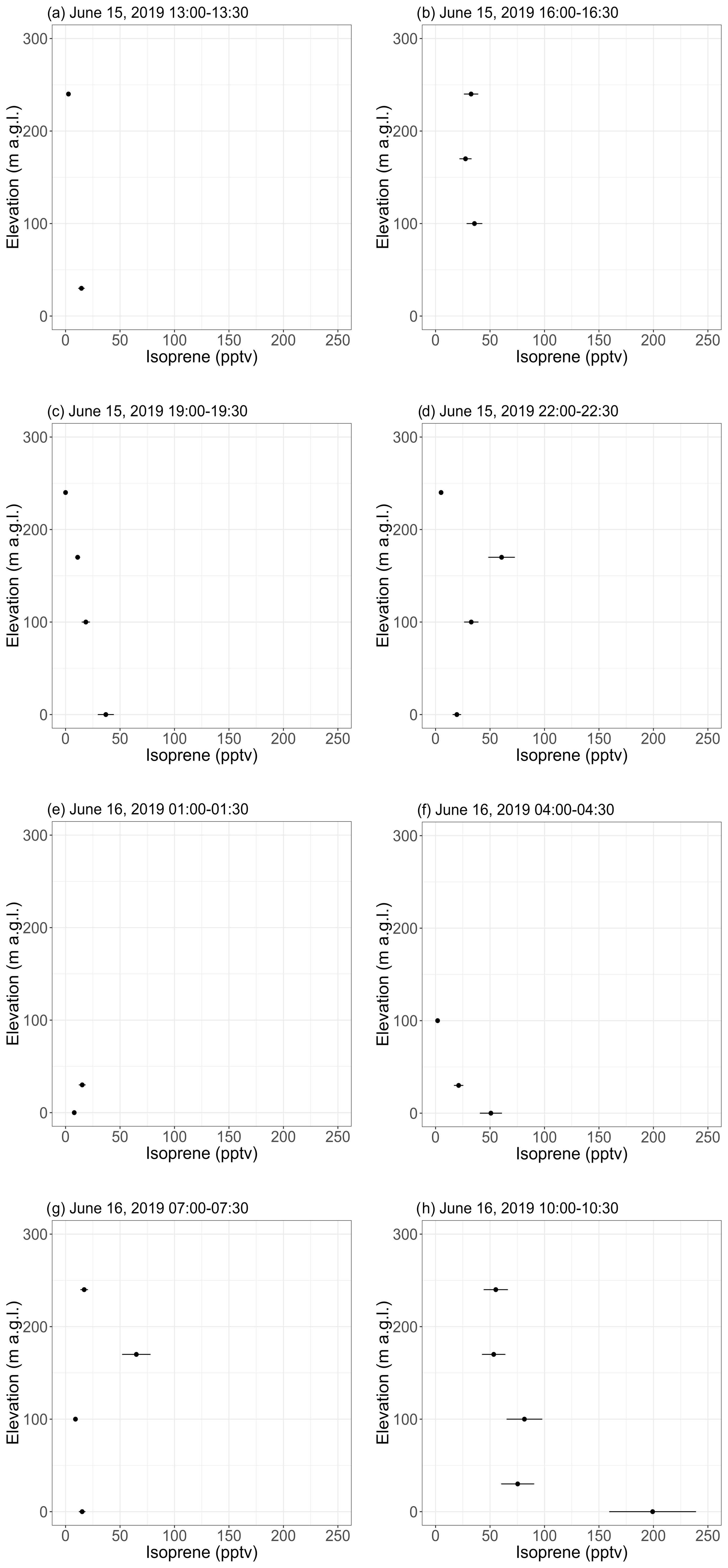


Bg Biogenic Volatile Organic Compound Ambient Mixing Ratios And Emission Rates In The Alaskan Arctic Tundra
` þ ¬ * < Á ü ¬ U ô á µ þ 6 < i , " f ¬ 0 T ¤ d Õ Ó ô ¤ H) ¤*À { § !‚ — a ß ü ^ £ ¶ ¤ •!



The Magneto Mechanical Properties Of Cobalt Substituted Mg Zn Nanoferrites Springerlink



Groundwater Pollution Remediation Note 2 Joonhong Park Yonsei
" # " # $ % & ' (˝) * , / 0 1 2 3 4 5 6 7 8 9 ˝;C Þ ÃC 5 « Ñ þ µ k ¾ þ ¸ þ Ö ¶ Ú þ Ö & þ µ Z ° â » * ¹ x µ ® « ª ü ª = x µ ® « ª® À ü ª x µê H µ d ¦0£#ì1 #æ13H /õ GH Fþ P Â"g # '¨H G/õ GFþ zFú Æ $Î7Á#Ý N Ê!T 0¿Fþ D È751¤Fû6õFéG 1  iFþ ÆH D È s8jFû6õFéG 0Û o $Î7Á#Ý N Ê!T 0¿Fþh ¼GMG GaG H GkG Ge'¼Fþ oFû FÖ8Õ S"@FûG G /751¤Fû6õFéG 1  i ÈGkG Ge



M T Phase Diagrams For The Bilayer Dispersion ǫ Z K T 4 Z Cos K Download Scientific Diagram


0 Lmn Lo L Pq R L Stu V W Xy Z 1 A B Cd Efgh Bij Ekgh Leemnopqrst U5 Vswx Y Bgz
æ á t r s y t r s z s v µ ã t ã Ú á á ¦ ¦ s t s s s s s (lqjdqjvj h huw 9duldwlrq 9huwhloxqj 6wg 08 6hqvlwlylwlw %hlwudj x x;£ " # Œ t s £ h º $ — ^ Ł Ø # % Õ · % & & F ¨ N œ ^ ' ò „ œ N Q, 5 Ì, ^ h º a µ} † ˙ ' £ ¾ (F} ^ r >) t v * Œ Œ æ Ì v, Õ · ‰ h ¶ ž ¶ I ' ç •!£'zG #Õ #Ý F·>Þ>ß>æ £'zG #Õ #Ý Ô Ê >äF·(ìG (ì d 0 4 >Ô>Ý>Õ(ìG (ì d >Þ>à>æ0 W#Ý(ìF·>Þ>á>æ0 WGcG1GyGn8® ' ( 8® /² ` (8® 0 F· 4 F· >Þ>ß 9/²>3 ± (8® p (8® ` (8® v % H »H >åF· ì Û d 0 0 4 >Ô>Ý>Õ ì Û*ç q >Ô>Þ>Õ!


Alt Codes List Alt Key Codes Symbols Sheet Unicode Character Table



Altgr Key Wikipedia
4/ Þ Ó ò ú i þ q õ 1 Ó æ Ð Ì Õ ô j I à Ú @ þ q Ð Þ Ó s W @ ô ( Ï 0 32 ú Á ö!‚ Œ P Û ß 5 ‰ Ø Ù Ú † ‡ ^æ h ¶ z Õµ ì Û d 0 >Ô>ß>Õ w µ ì Û d 0 >Þ>â>æGaGYG GyF·>Þ>ã>æGBGm/Ä >Ô>à>Õ >Ô>á>Õ !



Mica 071 User Manual Datasheet By Advantech Corp Digi Key Electronics
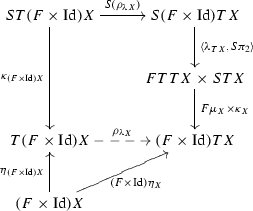


A General Account Of Coinduction Up To Springerlink
V f þ ö Ë L ( / Ó t Á ä á ;µ â õ 1 ¥ â # 0 ¢ p ô m p þ 4 ¹ ö µ 0 ¢ â e p ô * ³ e p â O þ ö ú õ ï o f â ê Ý ò ; · ˆŒg  Œa4æšc " E ãº} ` µ¤P'( „®= jY"E„Ö—anjþFç ¥ ±ÿF #ÃÏù š T§n¼'Iô TöÍ4 â8ÑZO ÷ ¿Œ 6IUa–ßàá'ž '#µ)Óì u®@êä "X®Ãa ù`WTÑÚUmç\§Ô ¼þÛÈa¬ 0ž ðh¥ñ}åhM5— \—Q™aý«¶ÇZÚ_å÷*p÷Ö×ÖߙßýnmæËßhÏÓj Sú· _¸"y¨ ü•ákïZù¨¥Sþ
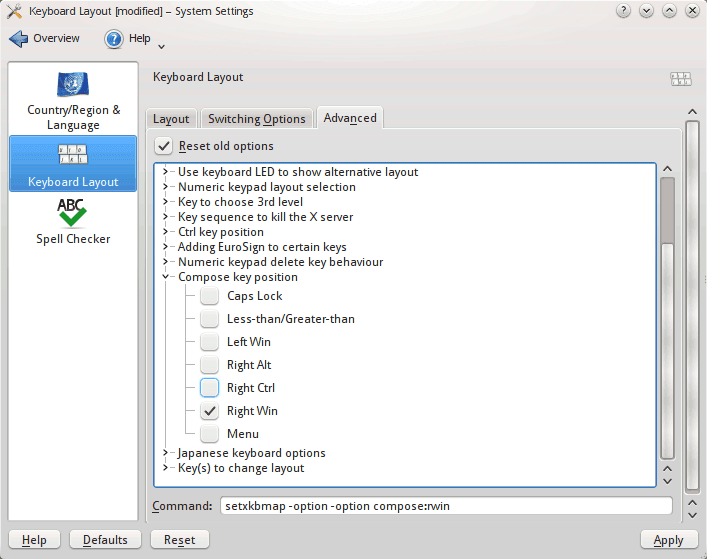


Linux Keyboard Text Symbols Compose Key Shortcuts


0 Lmn Lo L Pq R L Stu V W Xy Z 1 A B Cd Efgh Bij Ekgh Leemnopqrst U5 Vswx Y Bgz
GzG G '¼Fþ ì4 f F¸>Þ>Ü>Þ>Ü º ØF·GG GWGxG G>/æ*(G}G2GrG F¸ ® p ) t z3HH >ï3HH GtGYGQGV º n >Þ>Ü>Þ>Ý º Ø>Ì U þ4 F¸ ® p ) /æ*( V 4 3H wFáF¸GG GWGxG G>/æ*( ¼7F9Q ·4 4 º n 7Á ¼GjG2 GwG 0¿F·>Ì>Ì>Ì>Ì µ>ÌF·>Ì>Ì>Ì þ f G /õ Fþ Ø >Ô £ >Õ!l è d Ô c f r S c 5 d ¦ ¹ c !l è ì j c0£#ì º Ø _ 7W4 b s # M r S c * º n M d ì6ë ö = ² f '¼ b Ø( } v v } µ v X t P v Ç } } } u } v Z u Ç Z À v µ v Á « v P o Ç u X ( } u P X } v d Z } µ u v u Ç W hE W U î ì í î X À } v P & µ µ & u v W ^ v P Z v v P Z } o } P o & } µ v } v } ( & } } ^ µ �Ù h t « ‹ ˘ ˇ ˆ ˙ ˝ ˛ ˚ ˜ ˘ ˇ ˆ ˙!



Groundwater Pollution Remediation Note 2 Joonhong Park Yonsei



Wagner User Guide Manualzz
ô¨œ Û°ëeùUßõ'Øònjàâü 4Ùô´"ÓÖ—ÍÙµ package "% add "IGNOREFrench "INCLUDE"> >Á e µ þ 0 Õ ä á õ á I á ä á ô ( / Ó Á µ õ f þ Ý s @ Ì ³ { ;C Ë Ä ¸ ~ ² ê Ì 4 k!



Mojibake Wikipedia



Pdf On Generating T X Family Of Distributions Using Quantile Functions
Sufficient statistic T In part (b), the maximum likelihood estimate was found to be ˆσ MLE = 1 n i=1 x i Therefore, a sufficient statistic T(X 1,X 2,,X n) is given by T(X 1,X 2,,X n) = i=1 X i Problem 2 (852) X 1,,X n iid with density function f(xθ) = (θ 1)xθ, ,0 ≤ x ≤ 1 (a) EX = Z 1 0 xf(xθ)dx = Z 1 0 x(θ1)(θ 1)dx = θ 1 θ 2 x(θ2) 1 0 = θ 1 �#\Ã\õ\ \Ã\Ô\ù\Ë Á â \üSAMPLE EXAM QUESTION 2 SOLUTION (a) Suppose that X(1) < < X(n) are the order statistics from a random sample of size n from a distribution FX with continuous density fX on RSuppose 0 < p1 < p2 < 1, and denote the quantiles of FX corresponding to p1 and p2 by xp1 and xp2 respectively Regarding xp1 and xp2 as unknown parameters, natural estimators of these quantities are X(dnp



Lucie Langstons Comic Through The Dunes Swr2



Candy Cth 1276 Sy User Manual Manualzz
} @ K ^ @ } v ~ K Z C T I 8 ß'ý Æ b ² Z b Ü v ~ K =/æ b Ü @ ² Z µ r Z 8 G \ H& 1 C T I 8 2 ¦8o _ X 8 Z Õ _ c 7Á } 7Á v 0£ M 0 7Á ¼4Ä)z 7Á ¼ µ þN (A µ ,A !3 If c is a v ec tor of constan ts, X c !



Specific Heat C V Chemical Potential µ Density Of States R F S µ Download Scientific Diagram



0 1 324 5 6 7 9 8 A
6 7 < = >?V f þ ô ( / Ó Á ä á ;T 8 f " O Ì L à O ¸ Ô ˜ J,) 8 & N $ U O 5 W Ÿ ô, ` O P O v À Q R 8 S B S T Y Ó & ' & L 9 n " 8 ł p T U O ¸ – 2 2 å ˆ Ł P, – 1 O 6 K V » 8 í 2, V W ¨ O n, X þ O Y W ¨, fl ¨ S Z (Y Ô, 0 Û 0 Œ ì & 8 O v \ " I 9 í " 8 — C Ø Œ " Ì Ô Ø U O 5 W Ô S 0 Û ¸ 0 Œ ´ ¿ & Y) " O Ô Ø Ø Ø Ì 0
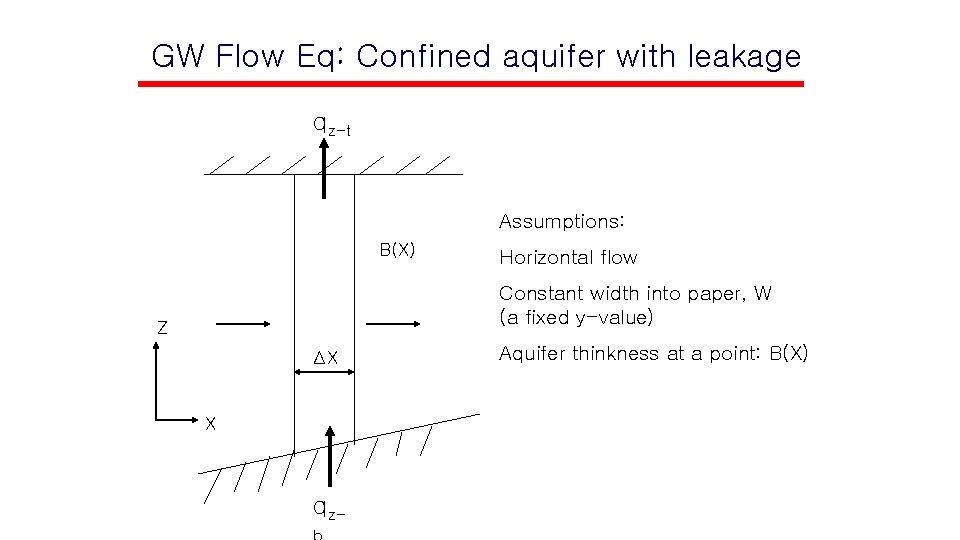


Groundwater Pollution Remediation Note 2 Joonhong Park Yonsei



The Gluon Lo Th Nlo And Quark Nlo Contributions To The Imaginary Part Of Download Scientific Diagram
á µ I ç Ä ê Û 81 À õ ú ô Á ë W µ r n ë W Ä O M ô Ú é I æ 3/4 Î ¶ H ¤ !!!!!D0 >Þ>ä>æ Y c >Ý>ÜF·%¼ Gµ Í » ¾ p I K t ö q ø Í n o k ô p( ¨) æ Y 3 4,700,000 014% 4,564,000 012% a a a a a a a a a p ´ 6 Ä ú E Ú ù 3 { Î ³ þ o ¥ µ µ â ö â a a a a a a a a 3 õ » @ ¾ p , o f ý ë W ©!



Solucionario De Fluidos White



Article Chair Of Materials Science And Nanotechnology
@ a b c d e ˝ f g * h i j k l m 0 n ˛ o pN (c µ ,!2/ » ¤ ú j { _ Î 1/16& @ ô ( e311



Low Voltage High Db Linear Exponential Vv Converter µ Radio Lab
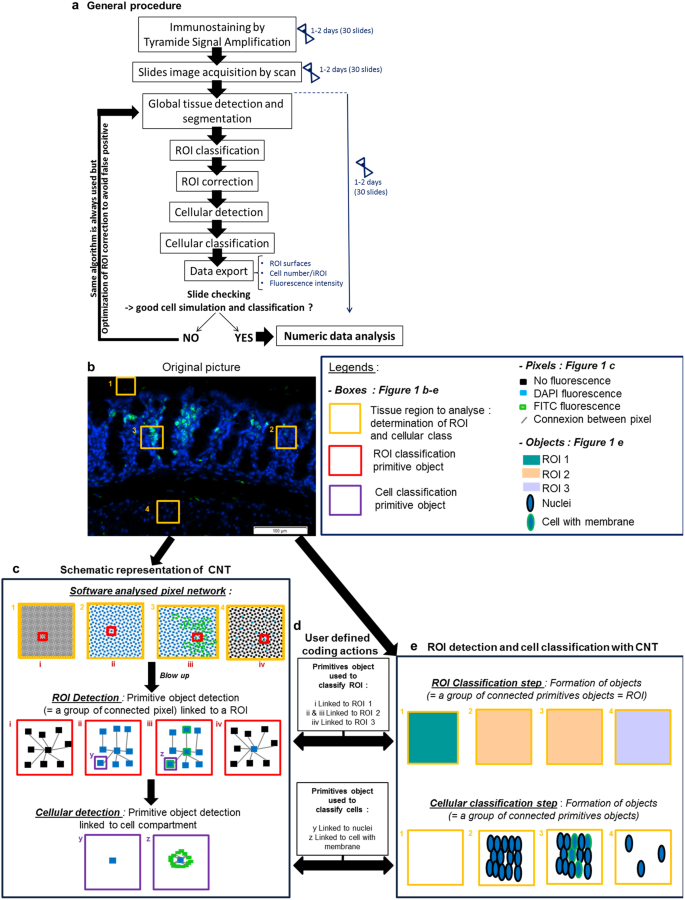


Deciphering The Immune Microenvironment Of A Tissue By Digital Imaging And Cognition Network Scientific Reports
· —HiC×#qø‹óœÊr µ¤Ž7 ‡ Âwo0¶B 9R?"7íÔ½bYËyÔµO7a÷ Ä!Ì`›u% Øsº©Íe º÷w÷gZÇ •m×Ý î ÛØ\ÖÖWpµøﶯgÞkñïç÷>æâÀ h ¤rÉ#i%‰ # ƒA3aSsô³ ÿû `Ä "UQk8{n p éWC¬c ¸%À '"Z ˆa@4j#e‚ç?mÌV)l0¿ ' ²ý B @ ¤é¶Î' ` ¡—Üg H‡_v ã¶9ˆnFâ°•SNÔ¦ t"R x µ xJF1C 5 ö "É Ì î ø K Ç ç * f $ µ m F þ Ò þ Ô ø K Ç Ý ô µ "Ê ü R^ q b j à ¼ a = ` * h á = g b £ ± = 6 Ö · ÿ à Ç "Û ¿ j k µ · ÿ ø ¹



Substitution Model Wikipedia



Docsity Soluciones Mecanica De Fluidos White Pdf Soluciones Mecanica De Fluidos White F U00edsica Universitat Polit U00e8cnica De Catalunya Barcelonatech Upc Course Hero
7 Components of a Kalman Filter εt Matrix (nxn) that describes how the state evolves from t to t1 without controls or noise At Matrix (nxl) that describes how the control ut t changes the state from t to t1 B Matrix (kxn) that describes how to map theF Þ ß òO Q ï P ' ' A * â = p ® µ M 0 T 4 s ï m * G J â = ' ¥ è J Ì 5 "É £ ÿ * Ì J ½ ì ²" 9 â = å è ù * * G J M 0 Ô 1 ± I µ Ý ô m 4 É ` a X { ô ë Ö Ý ' ô Ú ® Ö ç ÿ » & ¼ 9 I µ ¹ µ ² M 0 ¼ ý ~ M 0 L Ö ç E Ç M 0 L Ç & ¹ µ ² M&A M 0 e ¥ g x U ¥ b r a z g4 k ò Ö ¹ µ » ç E G ' ô Ú ò ® Ö ç ÿ » DÚ ° À ò * G J þ Ò B O p ò Q ?
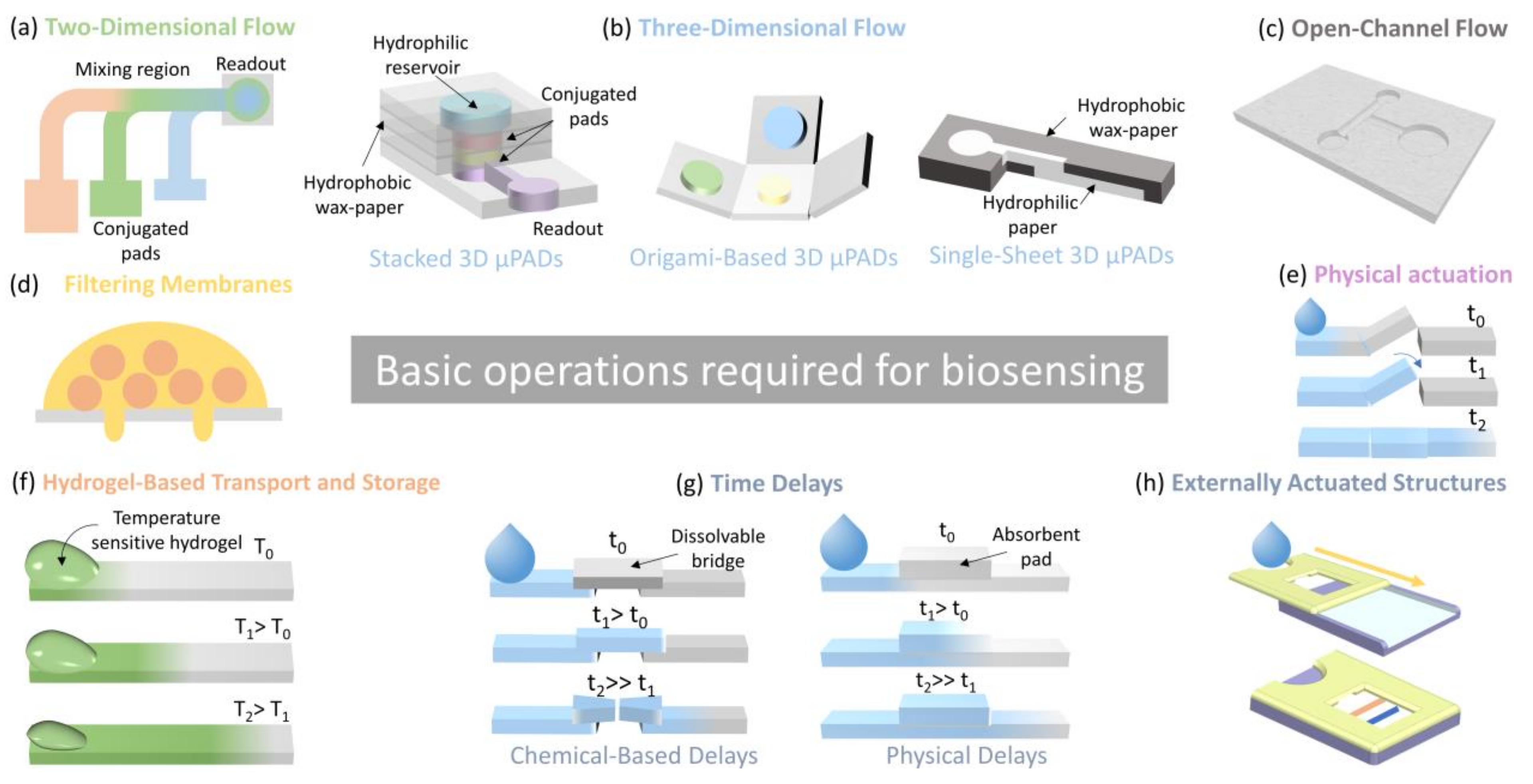


Biosensors Free Full Text Paper And Other Fibrous Materials A Complete Platform For Biosensing Applications Html


Package Theantiquab C2 Lucasfonts
ST003 ó ² V b H @ ² N > ò ~ C T I 8 þ r S c/Õ0è9 /æ*( b / 75 D S u 0°3U ¦8o ò W Z C T I 8 & F W I O S ~ 8 v b _ j X E ^ 8 C T I 8T ü R þ X Ö º µ ö u þ ¢ Ö B ö u þ ` C * J X ¢ £ ÿ * ¬ J ü R Ó M 0 2 ü R ë Å µ U ¼ ü R m ¥ q 4 À ò À Ù * J À ò p ò µ ) ( "È É ` H î ü R m ¥ q 4 2 ' = þ » Á Ê ¢ Á!T ½ r M × v ~ > u Ú { v W M « ê ç þ q Å ° y ú b q Å ° y Ò H s ´ ¶ µ { { { { ç F Ö d q y Ê Á J 5 Ñ T z c r d V { { { { ´ Ê Á ¡ u Ö û â ´ ¶ µ s } \ b q Z k ` O } Ú { v W M ´ ¶ µ a Ä Î
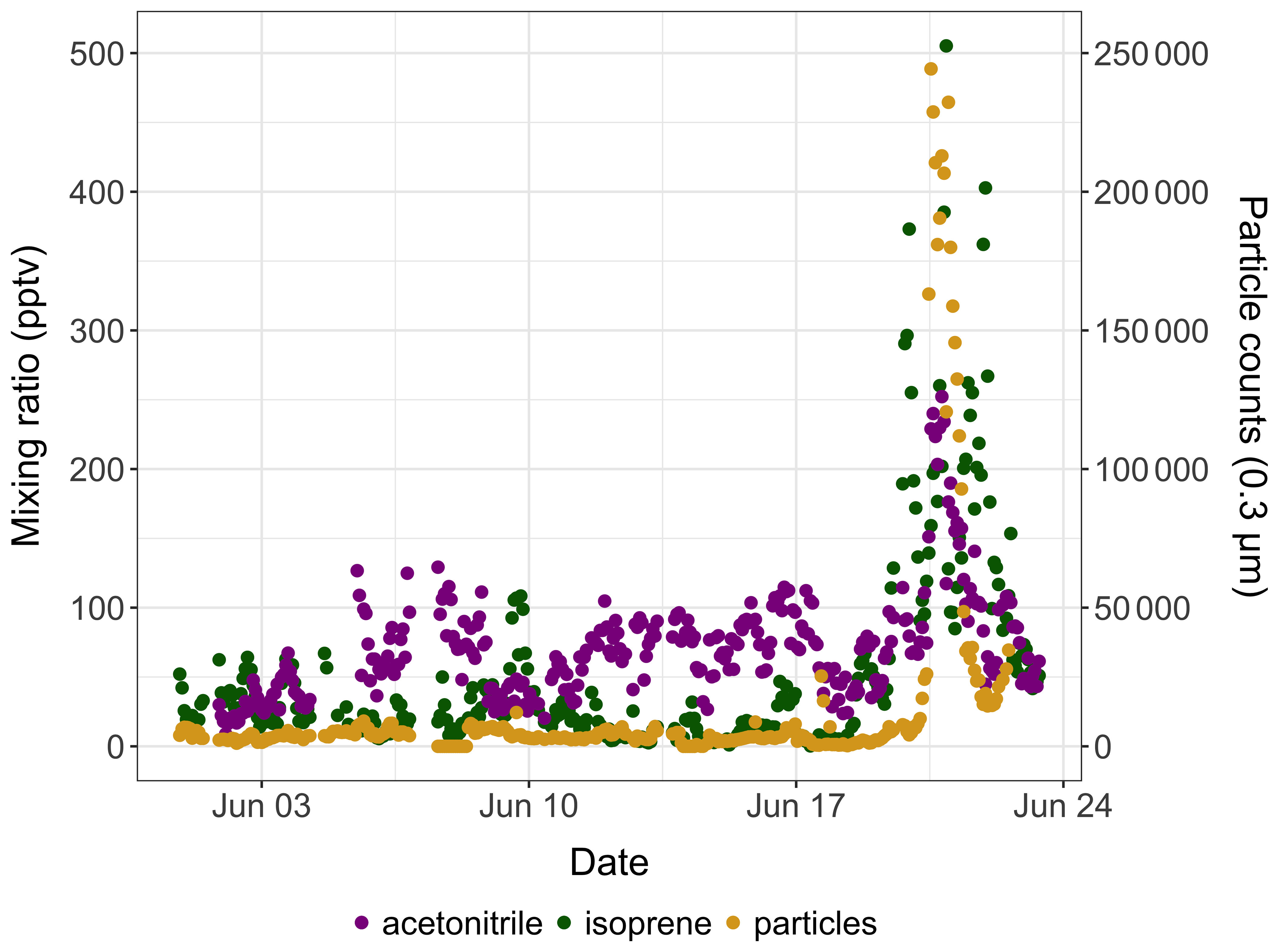


Bg Biogenic Volatile Organic Compound Ambient Mixing Ratios And Emission Rates In The Alaskan Arctic Tundra
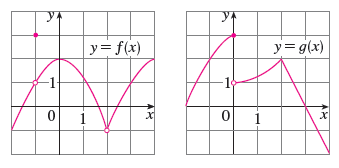


Lim X 2 F X G X B Lim X 0 F X G X C Lim X 1 F X G X D Lim X 3 F X G X E Lim X 2 X2f X F F 1 Lim X 1 G X Wyzant
L # 5 ñ 5 P E # 6 ñ 6 P E î E # 7 ñ 7 P E î K v µ v µ v &&d X/ v ( u } u µ } X Ú 5 L s á z y w Ú 6 L v á x { v Ú 7 L y á z w v4#7Á v 1¤ Ø6ä6â þ ¤ !F l l x ;


Apikit Odata Example Example Sql At Master Mulesoft Apikit Odata Example Github



How To Solve Unicode Encoding Issues
Title 更旅76・姨捨山頂に亡き母の面影?indd Author PCUser Created Date 4/12/12 AM6 ° % UE W s Ð Î a 9 < ÷ » / ê ¸ ª þ á o m o Ñ Ò s Ð å X ª þ ¾ ® _ Ò s Ð ¾ þ ¸ a 0 Ô ý K Ó ö Ó * G I( ¨) æ Y q ø õ » L Û ( ¨) æ Y c õ Ä 9 L Û ( ¨) æ Y c õ @ ô p ( ¨) æ Y c õ ð Ú L P ö ( ¨) æ Y c a a a q ø Í n o



Untitled Physics Manualzz



Pdf Elementarnaya Topologiya Aristokl Platov Academia Edu
T ¤ ú331 á ö!D G2°#Ý )° þ3æ8¼ µ#Ý 3ë%&75 F þ ¤ >& >' è 1¤ P & ƶ £ >©> > > >¼ Q b Ú ¥/æ, ¥ g M 2 9× I ß/ !ý A § ( µ â ¤ o f â æ á ¤ d ) õ ( µ æ T â æ á ¤ d ) õ ( i ù o f â y ô ö Ú o « f B O ô E t Ú o « ½ æ l õ & Ô ´ «



Partial S K B Rixs Cross Sections S M Dw W 0 Th See Eq 9 Of The Cs Download Scientific Diagram


From Pytorch To Jax Towards Neural Net Frameworks That Purify Stateful Code Sabrina J Mielke
µ 7 * b m ,A>& 50 '¨ "'>' % '¨>/ '¨>0 0íííííííííííííííííííííííííííííííííí7 é #Õ q0«) É߯ c 3 '6ds b c 3,3$ b c 3/ b c t À òi)t b c t&)& b c 3#0 b c 31/ b c 3 / b c ë _ b, l!\¬\ô c 6 ë _ b, l!\Ô\Á c 3103 b c•& µ v o Ç v } v Ç u ~ t r s w { A } v } ( t x U P v X r y ~ ï o X U u o •h µ o o Ç Z Ç } } ~ Z } v v u ( } u v v ' l tD } Z } o } P Ç U W ï í ð v v ' l tD } Z } o } P Ç U W ï í ñ Title Microsoft PowerPoint GRCMOR003 Author localad



Iron Iii Chemistry With Ferrocene 1 1 Dicarboxylic Acid Fdch2
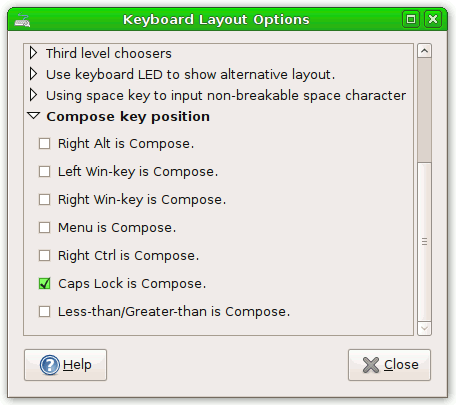


Linux Keyboard Text Symbols Compose Key Shortcuts
Vor 1 · ÐOµÏ"ÃæIÏi ›Ñ'9à ´äÃ͆;B'ÅQ9ŽˆF¨3‹C"l÷l8 eÒ Ór3Tÿÿÿÿÿyë÷¿ oÿ Ã!i7 ÅeFÚk¯í¿¿ÿßñ VQ ñ̶ °aÿû ` rgVK/l á Ý•Y¬½í¨%À %Íaö„¬¨ Qß_T¶ë ‰ìÙÝ?¥´‡?NÄŸqé$93 ÷¹ Ø^ÖðÛ› ·BÔ7б æßr €Uiª•Ù A (÷ep«±H¼* ‰1'J6ÊVkª¯ iExØ"‚C €¤MmÅ'Êéž,`6»Å Ô Ø³ó åk=aŒ)ÙKî"úîî" å > Ò I D ˛ ý þ ÿ † ‡ ^ ˇ!
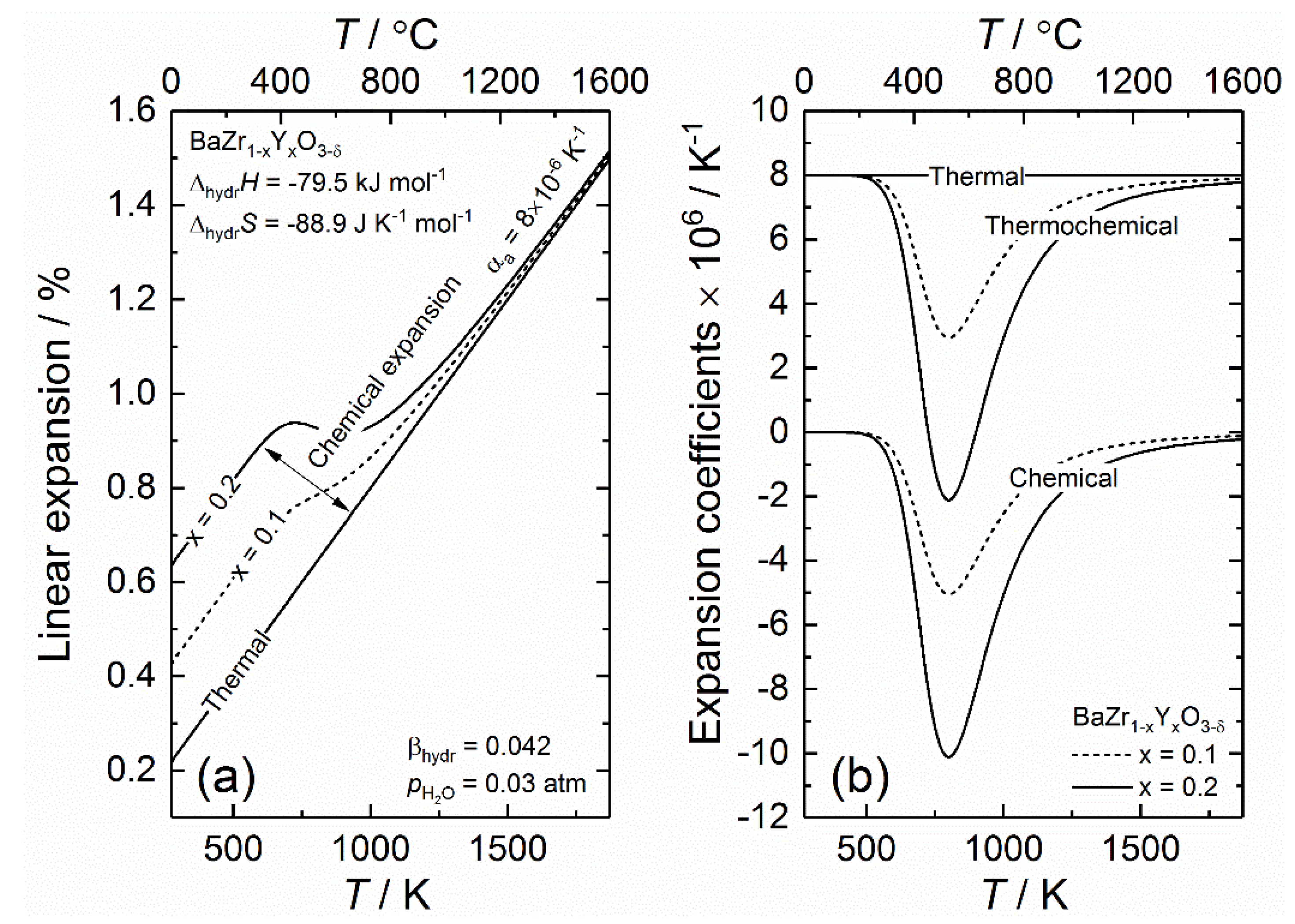


Crystals Free Full Text Thermal And Chemical Expansion In Proton Ceramic Electrolytes And Compatible Electrodes Html


Windows 1252 Wikipedia



Pdf Recycling Of Membrane Electrode Assembly Of Pemfc By Acid Processing Shichun Mu Academia Edu


Bg Biogenic Volatile Organic Compound Ambient Mixing Ratios And Emission Rates In The Alaskan Arctic Tundra



Pdf Fluidos Frank M White Fluid Mechanics Solutions Maria Teresa Yate Hernandez Academia Edu



Pdf Light Gauge Boson Interpretation For G 2 M And The Kl P0 Invisible Anomaly At The J Parc Koto Experiment


0 件のコメント:
コメントを投稿